32 Visualizing Time Series Data

Kate Lassiter

32.0.0.1 Starting Point

Same exploratory questions as with any new data set:

• Strongly correlated columns
• Variable means
• Sample variance, etc.
  

Use familiar techniques:

• Summary statistics
• Histograms
• Scatter plots, etc.

Be very careful of lookahead!

• Incorporating information from the future into past smoothing, prediction, etc. when you shouldn’t know it yet
• Can happen when time-shifting, smoothing, imputing data
• Can bias your model and make predictions worthless

32.0.0.2 Working with time series (ts) objects

Integration of ts() objects with ggplot2:

• ggfortify package
  • autoplot()
  • All the same customizations as ggplot2
  • Don’t have to convert from ts to dataframe format
• gridExtra package
  • Arrange the 4 ggplot plots as a 4-panel grid
• grid package
  • Add title to the grid arrangement

dax=autoplot(EuStockMarkets[,"DAX"])+
  ylab("Price")+
  xlab("Time")

cac=autoplot(EuStockMarkets[,"CAC"])+
  ylab("Price")+
  xlab("Time")

smi=autoplot(EuStockMarkets[,"SMI"])+
  ylab("Price")+
  xlab("Time")

ftse=autoplot(EuStockMarkets[,"FTSE"])+
  ylab("Price")+
  xlab("Time")
grid.arrange(dax,cac,smi,ftse,top=textGrob("Stock market prices"))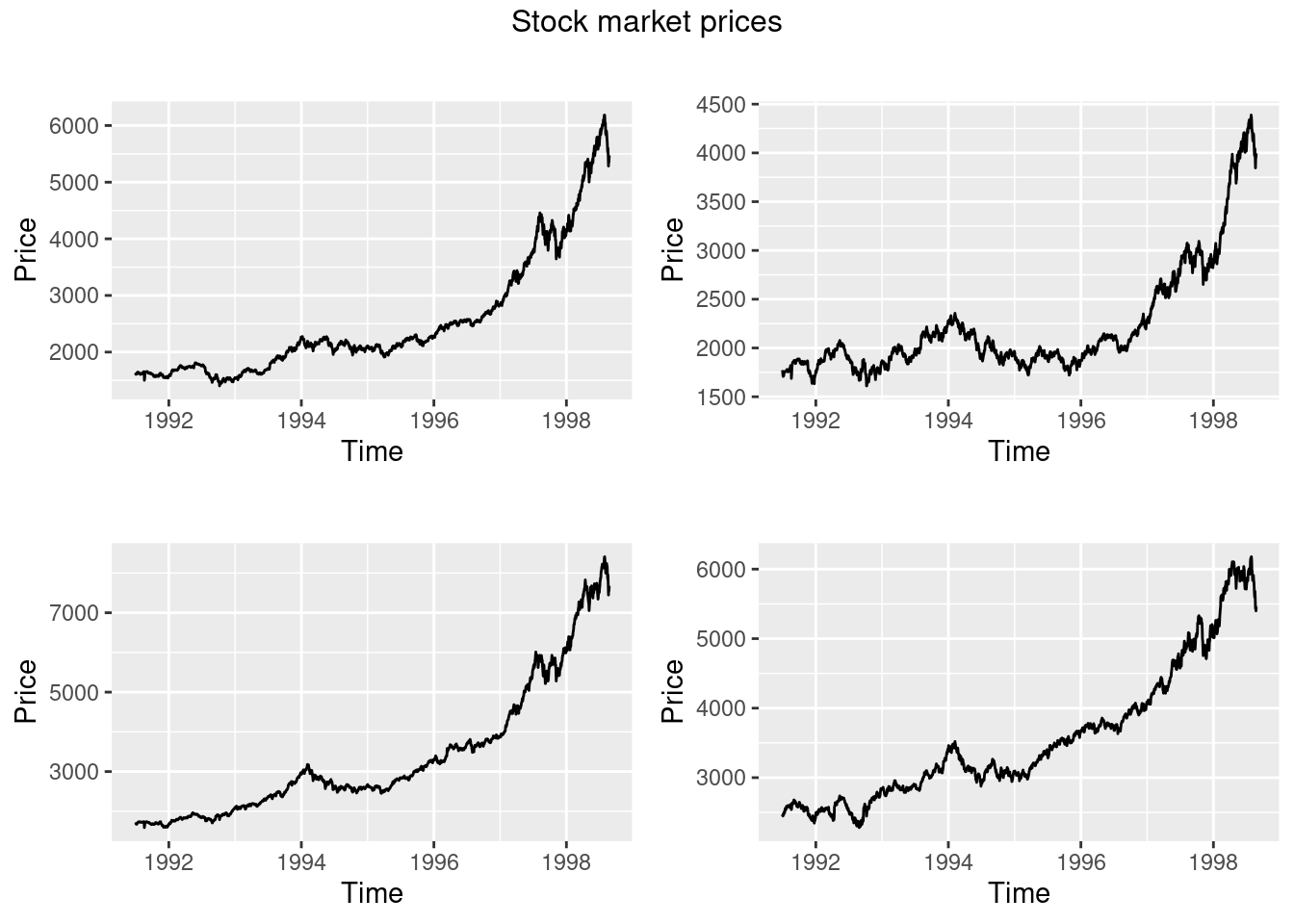

32.0.0.3 Time series relevant plotting:

Working with the data:

• Directly transforming ts() objects for use with ggplot2:
  
  • complete.cases() to easily remove NA rows - prevent ggplot warning
  • avoid irritations of working with ts objects

Looking at changes over time:

• Plot differenced values
  • Histogram/scatter plot of the lagged data
  • Shows change in values, how values change together
  • Trend can hide true relationship, make two series appear highly predictive of one another when they move together
  • Use base package diff(), calculates difference between point at time t and t+1

new=as.data.frame(EuStockMarkets)
new$SMI_diff=c(NA,diff(new$SMI))
new$DAX_diff=c(NA,diff(new$DAX))

p1 <- ggplot(new, aes(SMI,DAX))+
  geom_point(shape = 21, colour = "black", fill = "white")
p2 <- ggplot(new[complete.cases(new),], aes(SMI_diff,DAX_diff))+
  geom_point(shape = 21, colour = "black", fill = "white")

grid.arrange(p1,p2,top=textGrob("SMI vs DAX"))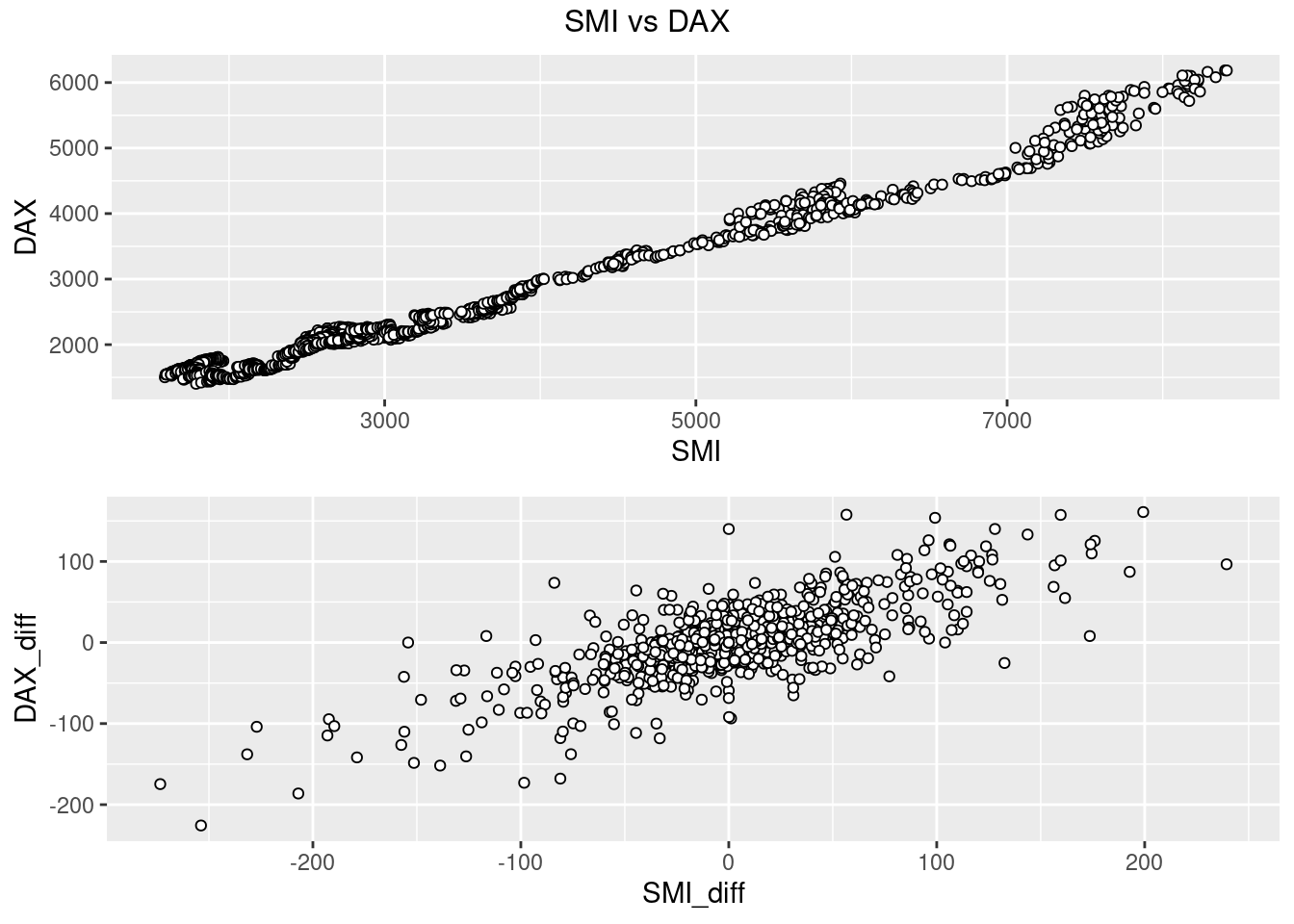

Exploring Time Lags:

• Lagged differences:
  
  • Time series analysis: focused on predicting future values from past
  • Concerned whether a change in one variable at time t predicts change in another variable at time t+1
  • lag() to shift forward by one
  • Showing density using alpha

new$SMI_lag_diff=c(NA,lag(diff(new$SMI),1))
ggplot(new[complete.cases(new),], aes(SMI_lag_diff,DAX_diff))+
  geom_point(shape = 21, colour = "black", fill = "white",alpha=0.4,size=2)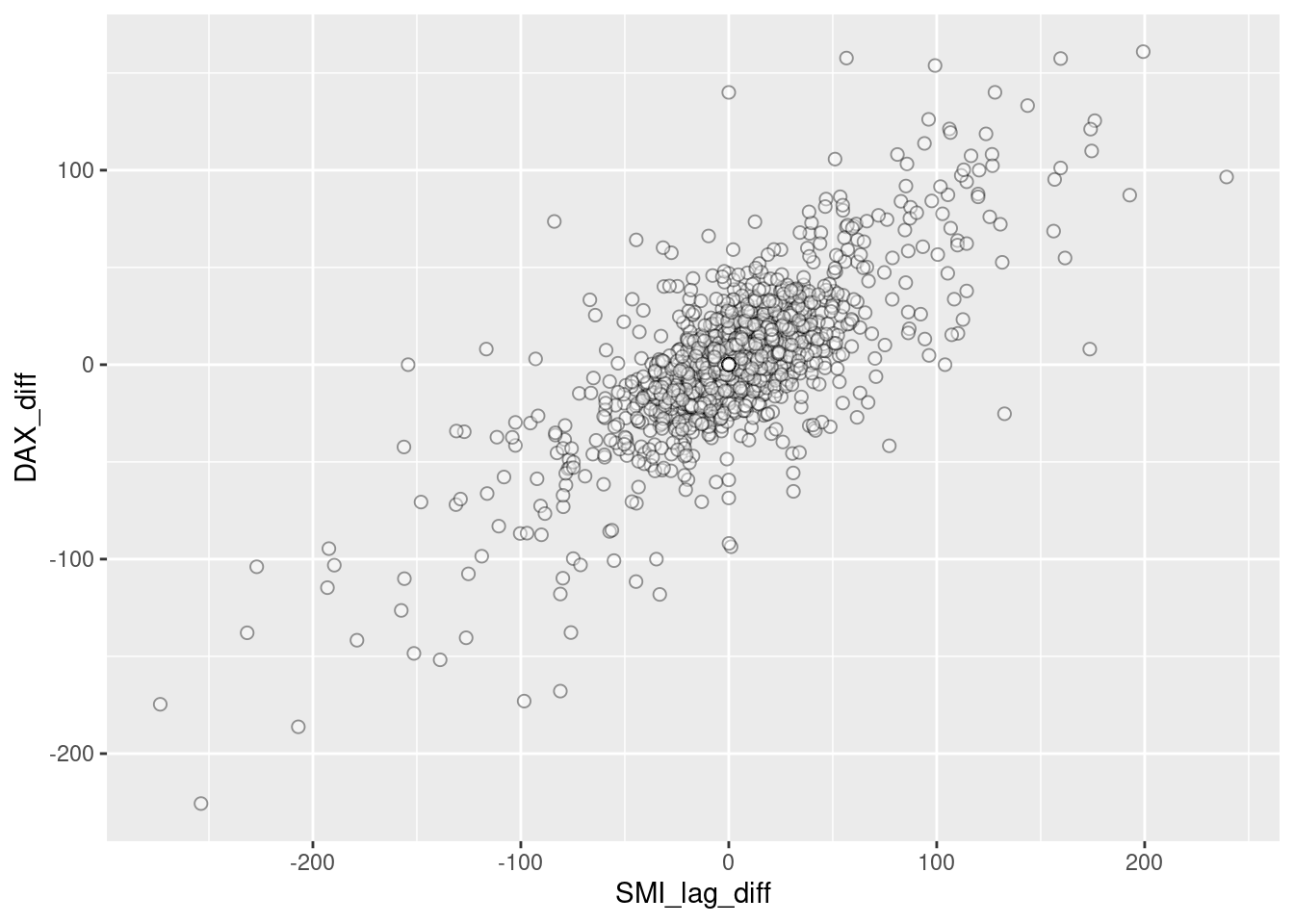

Now there is no apparent relationship: positive change in SMI today won’t predict positive change in DAX tomorrow. There is a positive trend over the long term, but this does little to predict in the short term

Observations:

• Be careful with time series data: use same techniques, but reshape data
• Change in values from one time to another is vital concept
  

32.0.0.4 Dynamics of Time Series Data

Three aspects of time series data:

• Seasonal:
  • Recurs over a fixed period
• Cycle:
  • Recurrent behaviors, variable time period
• Trend:
  • Overall drift to higher/lower values over a long time period
    

32.0.0.4.1 Line plots

Discover patterns through visual inspection:

autoplot(AirPassengers)+
  xlab("Year")+
  ylab("Passengers")

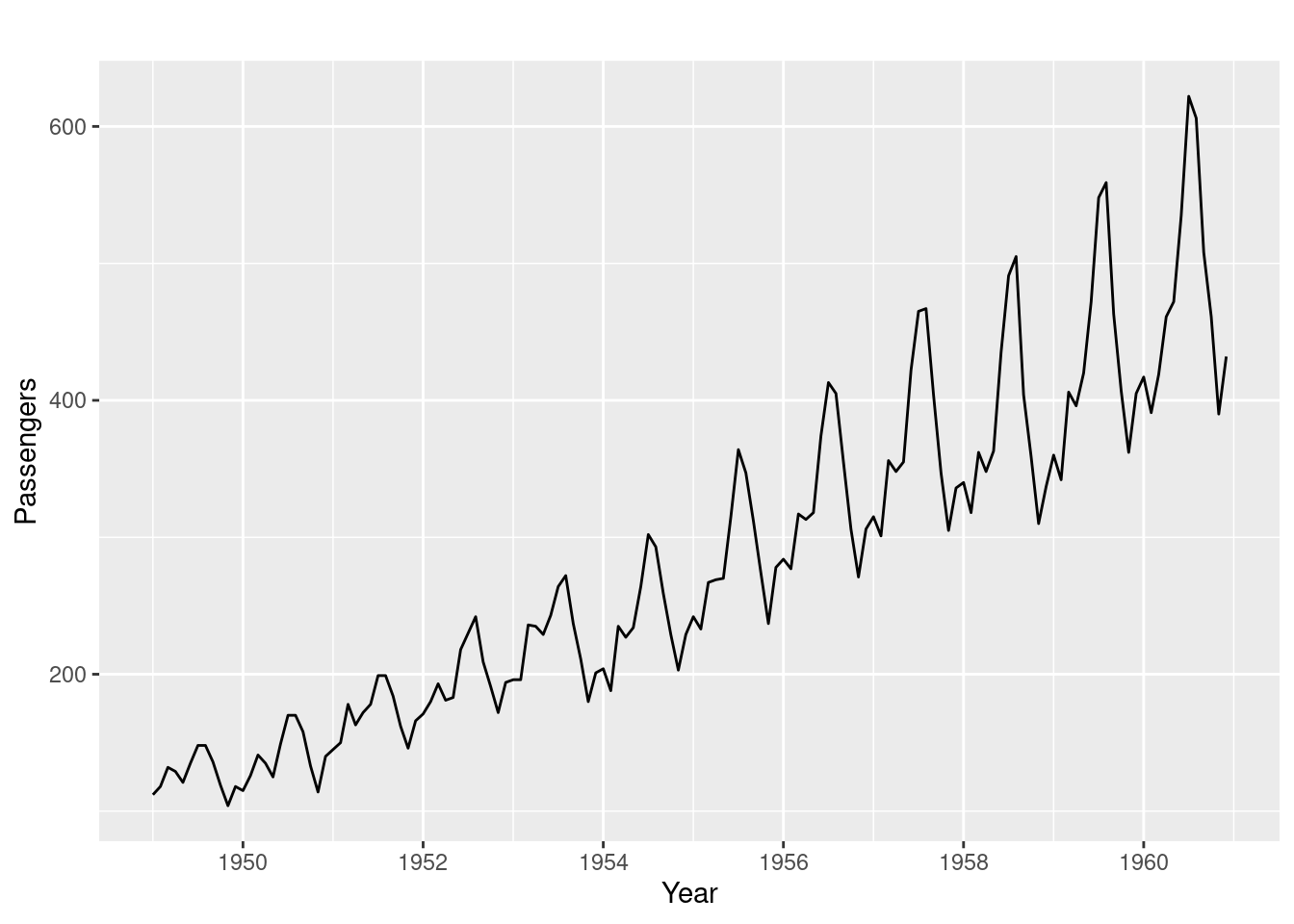
• Observations:
  • Clear trend
    • Consider log transform or differencing
  • Increasing variance
    • Consider log or square root transform
  • Multiplicative seasonality
    • Seasonal swings grow along with overall values

32.0.0.4.2 Time series decomposition:

• Break data into seasonal, trend, and remainder components
• Seasonal component:
  • LOESS smoothing of all January values, February values, etc.
  • Moving window estimate of smoothed value based on point’s neighbors
• stats package
  • stl()
    

autoplot(stl(AirPassengers, s.window = 'periodic'), ts.colour = 'red')+
  xlab("Year")

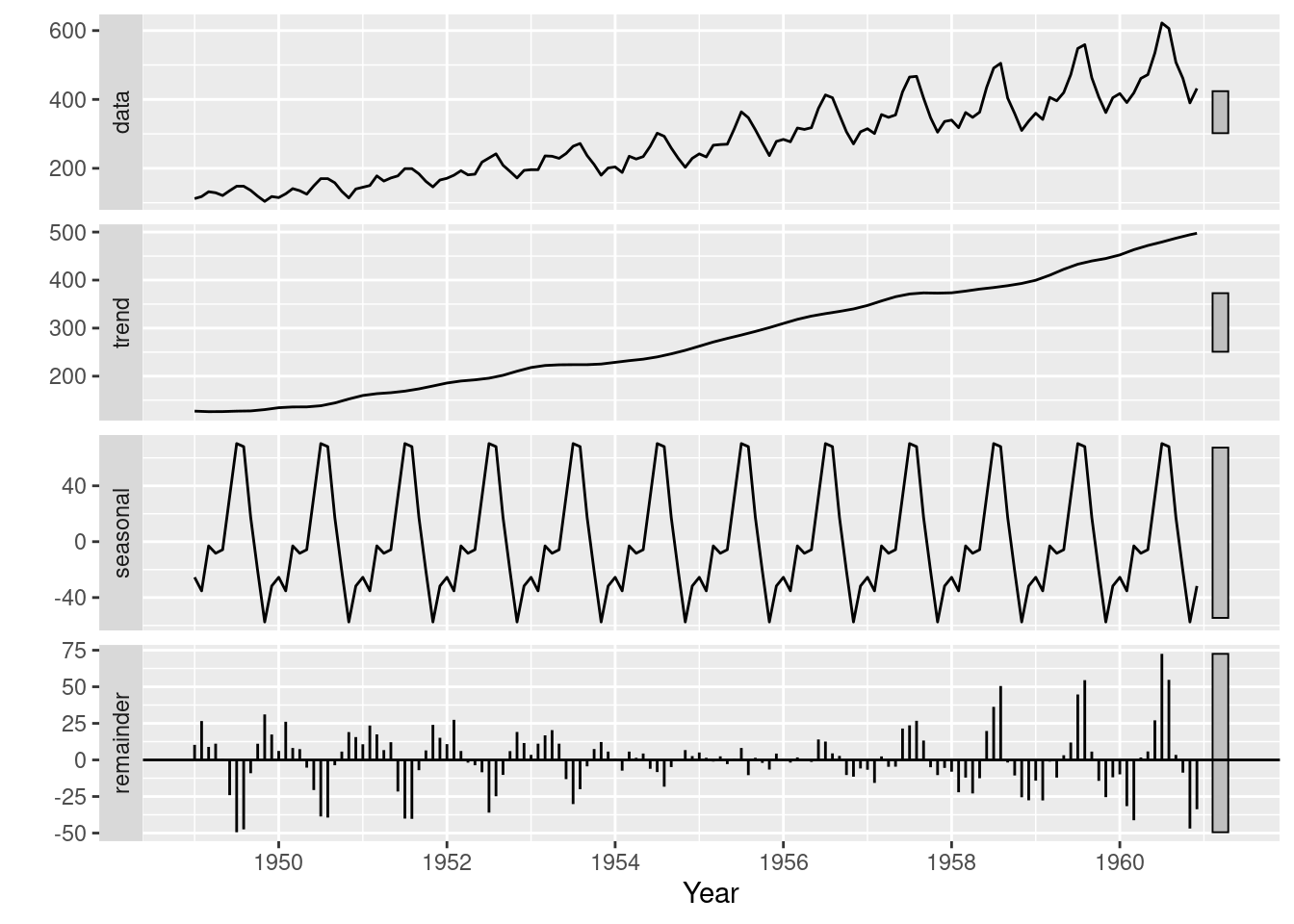
• Observations
  • Clear rising trend
  • Obvious seasonality
  • Difference between the two methods:
    • This particular decomposition shows additive, not multiplicative seasonality
      • But start and end time series have highest residuals
      • Settled on the average seasonal variance
  • Both reveal information on patterns that need to be identified and potentially dealt with before forecasting can occur
    

32.0.0.5 Plotting: Exploiting the Temporal Axis

32.0.0.5.1 Gannt charts

• Shows overlapping time periods, duration of event relative to others
• timevis package timevis()

dates=sample(seq(as.Date('1998-01-01'), as.Date('2000-01-01'), by="day"), 16)
dates=dates[order(dates)]
projects = paste0("Project ",seq(1,8)) 

data <- data.frame(content = projects, 
                    start = dates[1:8],
                    end = dates[9:16])
timevis(data)

32.0.0.5.2 Using month and year creatively in line plots

• forecast package
  • ggseasonplot()
    • X axis is months
    • Y axis is the variable of interest
    • Each line represents a year.
    • Shows if months exhibited similar/different seasonal patterns over the years
  • ggmonthplot()
    • X axis is months
    • Y axis is the variable of interest
    • Blue line is mean of each season
    • Black line is the values for every year for a single month

ggseasonplot(AirPassengers)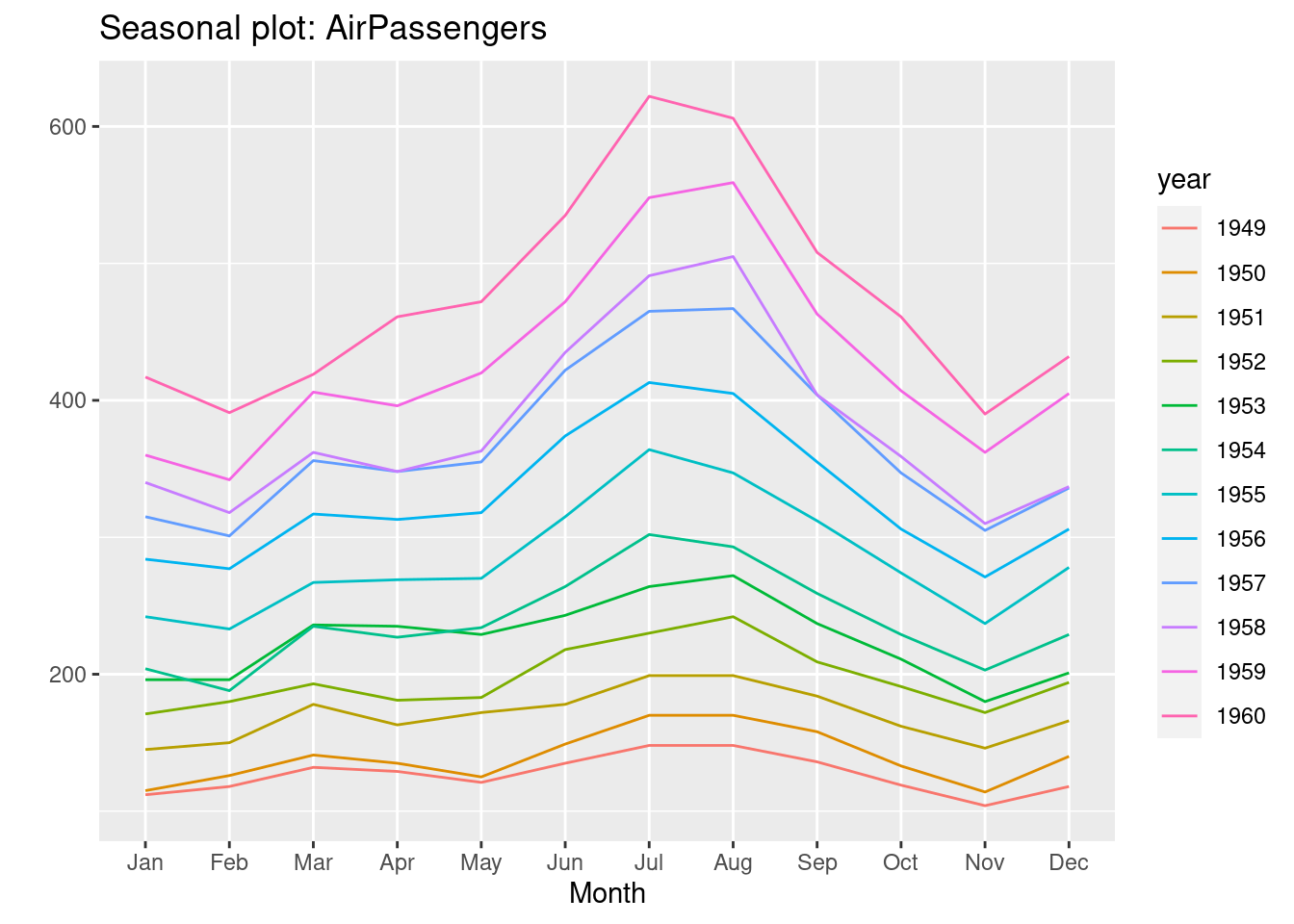

ggmonthplot(AirPassengers)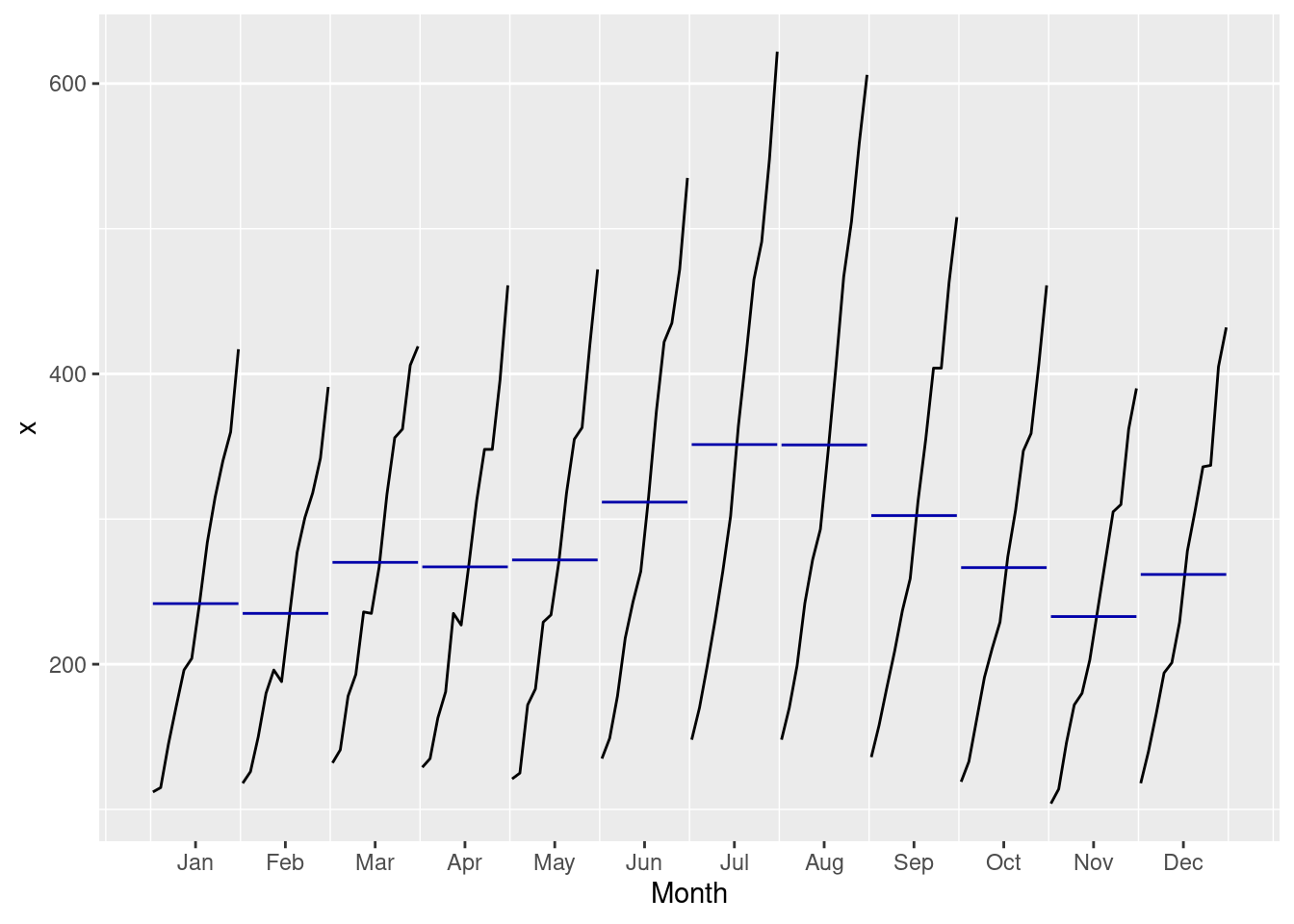

• Observations
  • Some months increased more over time than others
  • Passenger numbers peak in July or August
  • Local peak in March most years
  • Overall increase across months over the years
  • Growth trend increasing (rate of increase increasing)
    
    

32.0.0.6 3-D Visualizations: plotly package

• Convert to a format plotly will understand
  • Avoid using ts() object
  • Dataframe with datetime, numeric columns
  • lubridate package for date manipulation
    • year()
    • month()

new = data.frame(AirPassengers)
new$year=year(seq(as.Date("1949-01-01"),as.Date("1960-12-01"),by="month"))
new$month=lubridate::month(seq(as.Date("1949-01-01"),as.Date("1960-12-01"),by="month"),label=TRUE)
plot_ly(new, x = ~month, y = ~year, z = ~AirPassengers, 
             color = ~as.factor(month)) %>%
    add_markers() %>%
    layout(scene = list(xaxis = list(title = 'Month'),
                        yaxis = list(title = 'Year'),
                        zaxis = list(title = 'Passenger Count')))

• Allows a better view of the relationship between month, year, and number of passengers

32.0.0.7 Data Smoothing

• Usually need to smooth the data before starting analysis or visualization
  • Allows better storytelling
  • Irrelevant spikes dominate the narrative
• Methods:
  • Moving average/median
    • Good for noisy data
    • Rolling mean reduces variance
      • Keep in mind: affects accuracy, R² statistics, etc.
      • Zoo package rollmean() and rollmedian()
        • k = 7 is a 7 month rolling window
    • Prevent lookahead, use past values as the window (align=“right”)
    • gsub() substitute series names for a clearer legend
    • tidyr package gather()
      • Convert from wide to long, use this as color/group in ggplot2 geom_line()
        
  • Exponentially weighted moving average
    • Weigh past values less than recent
    • pracma package movavg() function
    • Useful when more recent data is more or less informative than the past
  • Geometric mean
    • Combats strong serial correlation
    • Good for series with data that compounds greatly as time goes on
    • Base R exp(mean(log())) and zoo package rollapply()

new = data.frame(AirPassengers)
new$AirPassengers=as.numeric(new$AirPassengers)
new$year=seq(as.Date("1949-01-01"),as.Date("1960-12-01"),by="month")

new = new %>%
  mutate(roll_mean = rollmean(new$AirPassengers,k=7,align="right",fill = NA),
         roll_median = rollmedian(new$AirPassengers,k=7,align="right",fill = NA))

df <- gather(new, key = year, value = Rate, 
                            c("roll_mean","roll_median", "AirPassengers"))
df$year=gsub("AirPassengers","series",df$year)
df$year=gsub("roll_mean","rolling mean",df$year)
df$year=gsub("roll_median","rolling median",df$year)
df$date = rep(new$year,3)

ggplot(df[complete.cases(df),], aes(x=date, y = Rate, group = year, colour = year)) + 
  geom_line()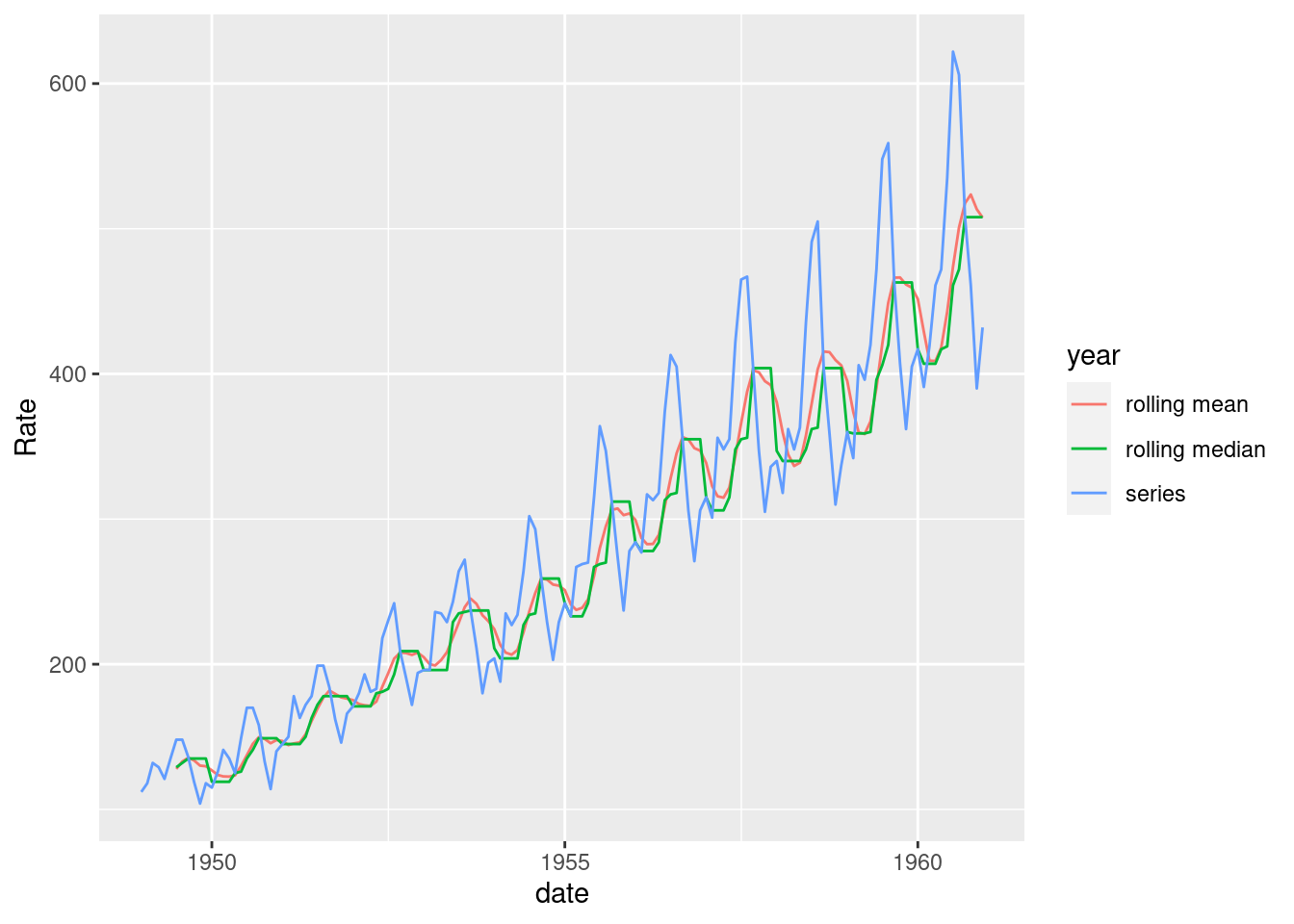

 

32.0.0.8 Checking Time Series Properties

32.0.0.8.1 Stationarity

• Many time series models rely on stationarity
  • Stable mean/variance/autocorrelation over time
  • Examine error term behavior
  • Can do this visually:
    • Look for seasonality, trend, increasing variance
  • Statistically:
    • Augmented Dickey–Fuller (ADF) test
      • Null hypothesis = unit root
      • Focuses on changing mean
      • tseries package adf.test()
  • Visual can be better:
    • ADF tests perform poorly on near unit roots, small sample size
    • Use both approaches
  • Remedies:
    • Difference the data to correct trend
    • Logarithm or square root to correct variance

new = data.frame(AirPassengers)
new$AirPassengers=as.numeric(new$AirPassengers)
new$date=seq(as.Date("1949-01-01"),as.Date("1960-12-01"),by="month")
new$diff_data=c(NA,diff(new$AirPassengers, differences=1))
new$diff_data2=c(NA,NA,diff(new$AirPassengers, differences=2))

g=ggplot(new , aes(date,AirPassengers))+
  geom_line(colour = "black")

g_diff=ggplot(new , aes(date,diff_data))+
  geom_line(colour = "red")+
  ylab("Difference Data")

g_diff2=ggplot(new , aes(date,diff_data2))+
  geom_line(colour = "blue")+
  ylab("2nd Difference Data")

grid.arrange(g,g_diff,g_diff2,top=textGrob("Airline Passengers"))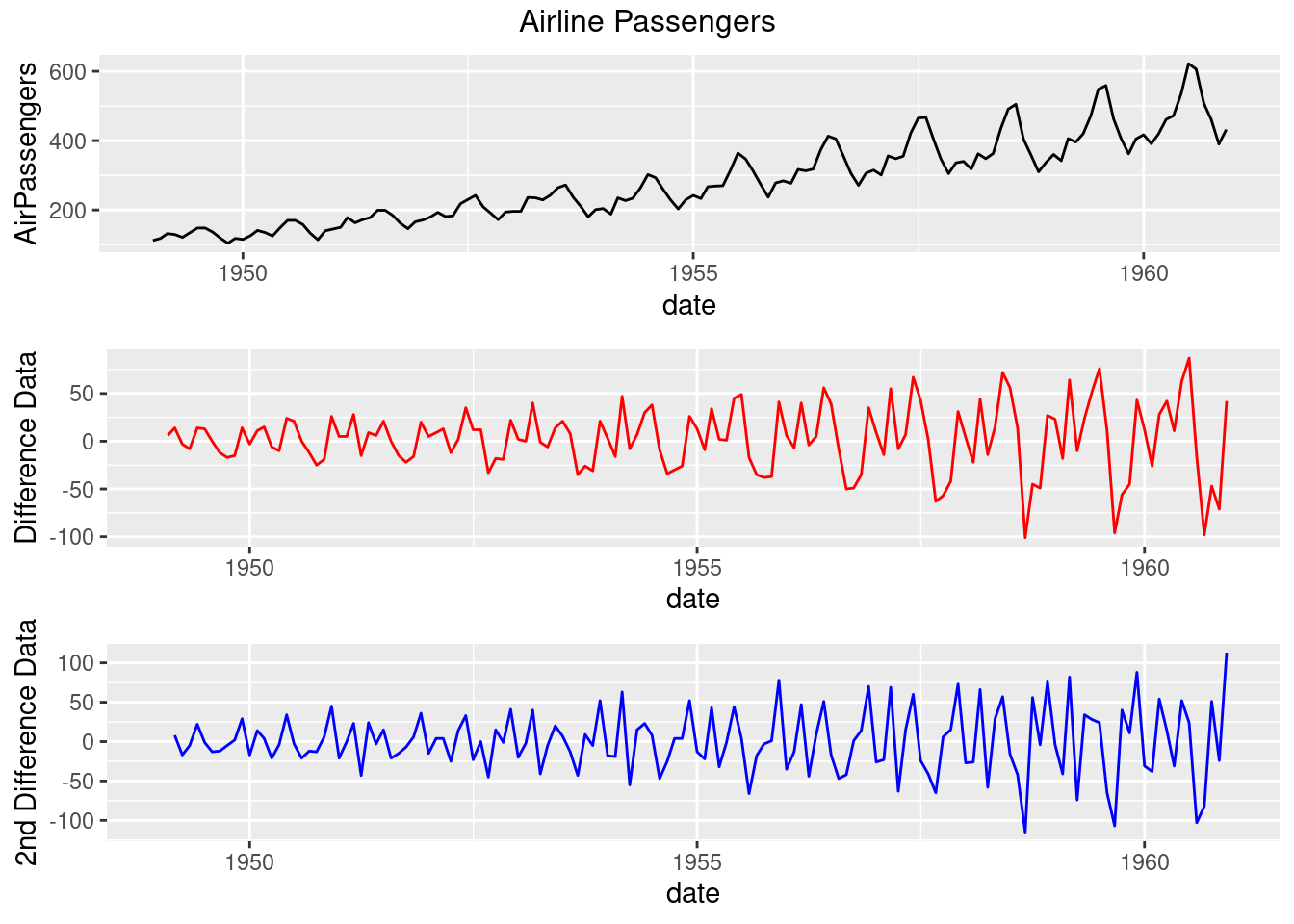

adf.test(new$AirPassengers,alternative='stationary')

## 
##  Augmented Dickey-Fuller Test
## 
## data:  new$AirPassengers
## Dickey-Fuller = -7.3186, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationary

adf.test(new[complete.cases(new$diff_data),3],alternative='stationary')

## 
##  Augmented Dickey-Fuller Test
## 
## data:  new[complete.cases(new$diff_data), 3]
## Dickey-Fuller = -7.0177, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationary

adf.test(new[complete.cases(new$diff_data2),4],alternative='stationary')

## 
##  Augmented Dickey-Fuller Test
## 
## data:  new[complete.cases(new$diff_data2), 4]
## Dickey-Fuller = -8.0516, Lag order = 5, p-value = 0.01
## alternative hypothesis: stationary

• Observations:
  • The data has clear trend and increasing variance
  • By using differencing, the trend is dampened
  • There’s still some increasing variance, so log transform might be the right choice
  • Things start getting muddied at second difference
  • ADF says that the original series is stationary based on small p-value
    • Visual inspection says otherwise

32.0.0.8.2 Normality:

• Many time series models assume normality
• This can be observed through a histogram or QQ plot
  • ggplot2 package geom_histogram()
  • stats package qqnorm() and qqline()
• If it is not normal:
  • Box Cox transformation
    • MASS package boxcox()
  • Be careful with transformations!
    • Are you preserving the important information?

ggplot(new, aes(x=AirPassengers)) +
  geom_histogram(binwidth =20,fill = "mediumpurple") +             
  xlab("Passengers")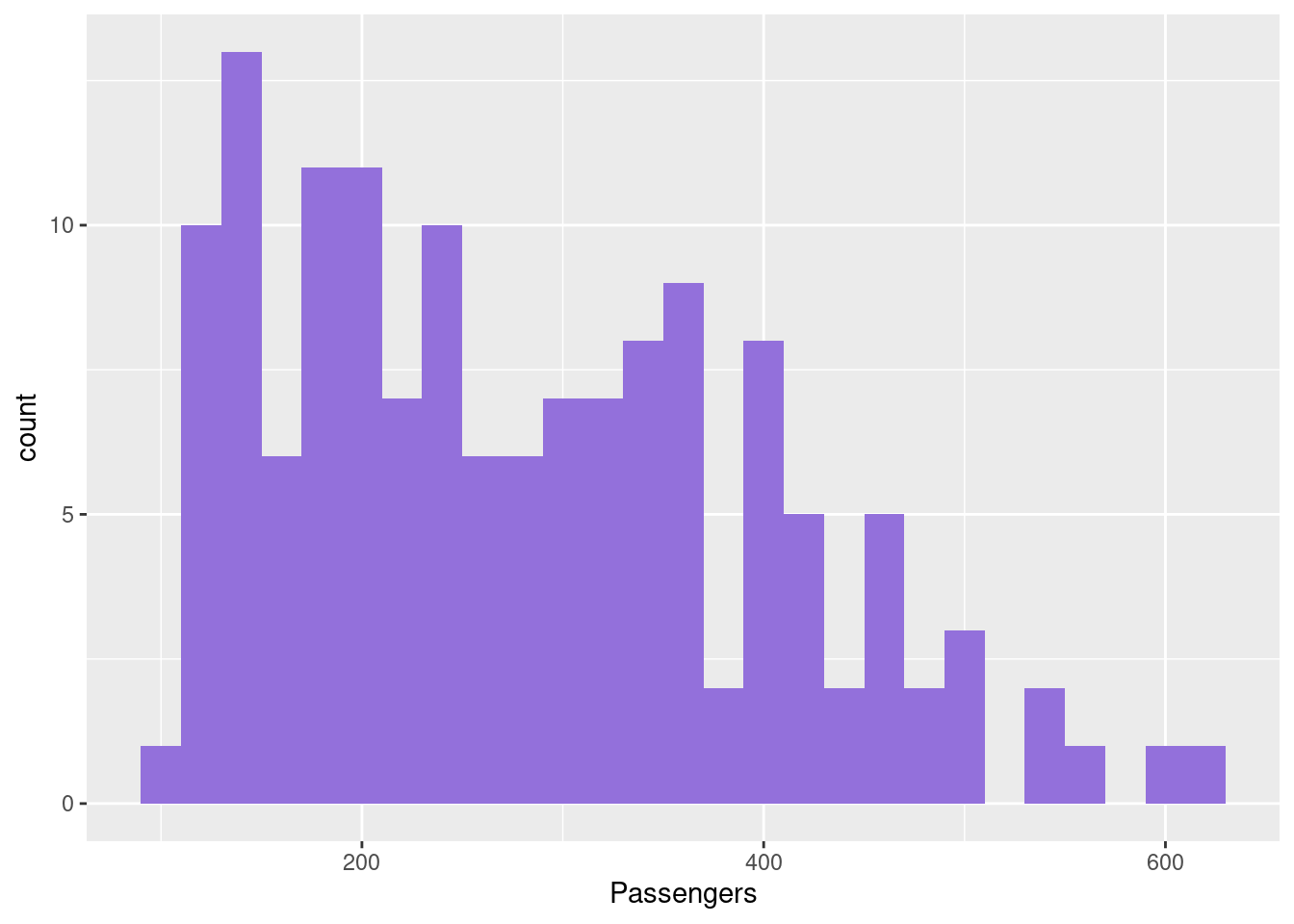

qqnorm(new$AirPassengers, main="Airline Passengers", xlab="", ylab="", pch=16)
qqline(new$AirPassengers)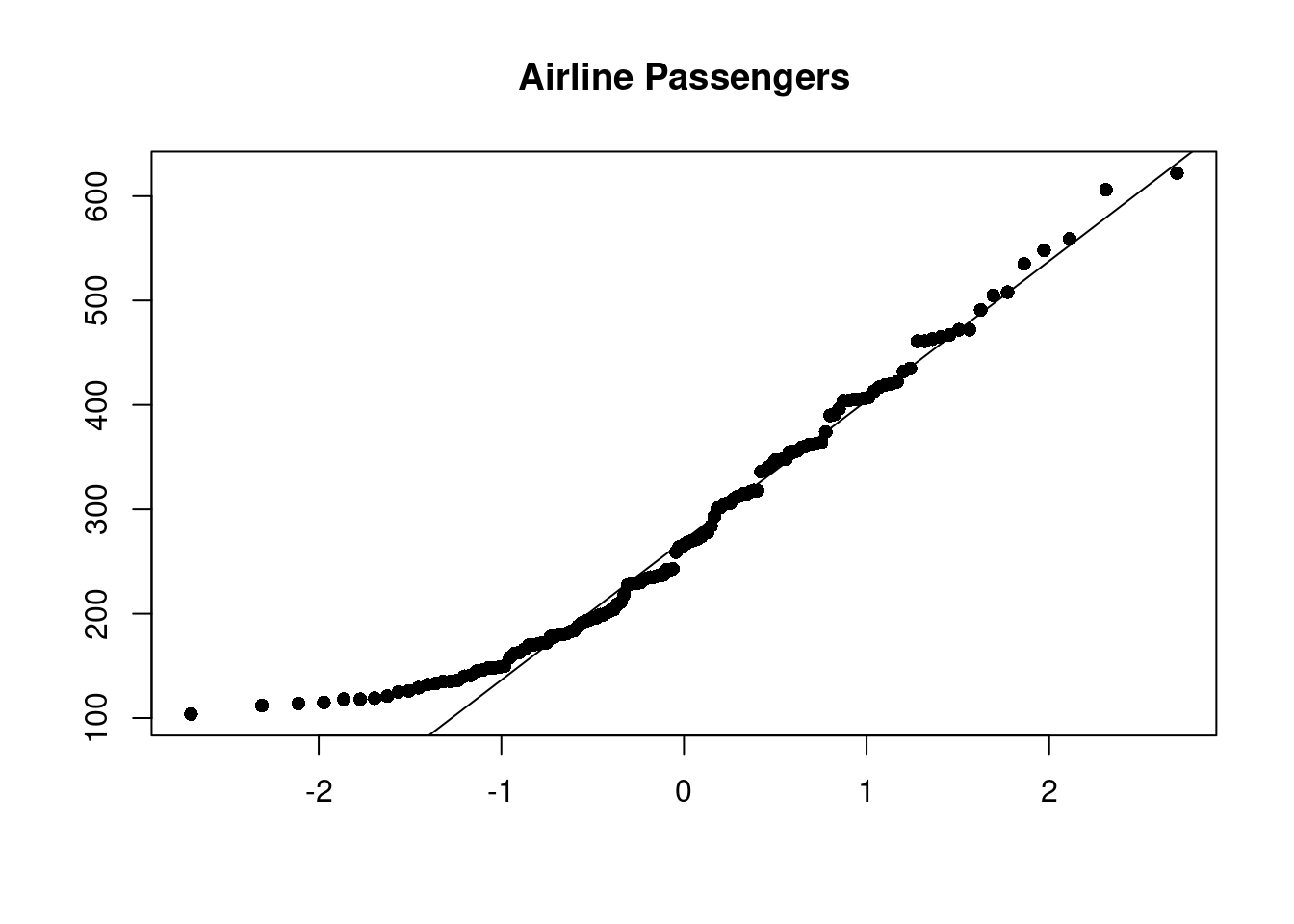

• Observations:
  • Data does not look normal: it is skewed
  • Even though this doesn’t capture the time aspect of the data, the input variable must be normal for many models

32.0.0.8.3 Lagged Correlations

• Autocorrelation Function
  • Correlation between two points in a time series in a fixed interval
  • Linear relationship between points as a function of their time difference
  • Common behaviors:
    • ACF of stationary series drops to zero quickly
    • For nonstationary series, value at lag 1 is large and positive
    • White noise will have 0 at all lags but 0
  • Significance of ACF estimate determined by “critical region” with bounds at +/–1.96 × sqrt(n)
  • forecast package Acf()
    • Y axis is the correlation
    • X axis is the time lag

Acf(new$AirPassengers,main='Passengers Autcorrelation Function')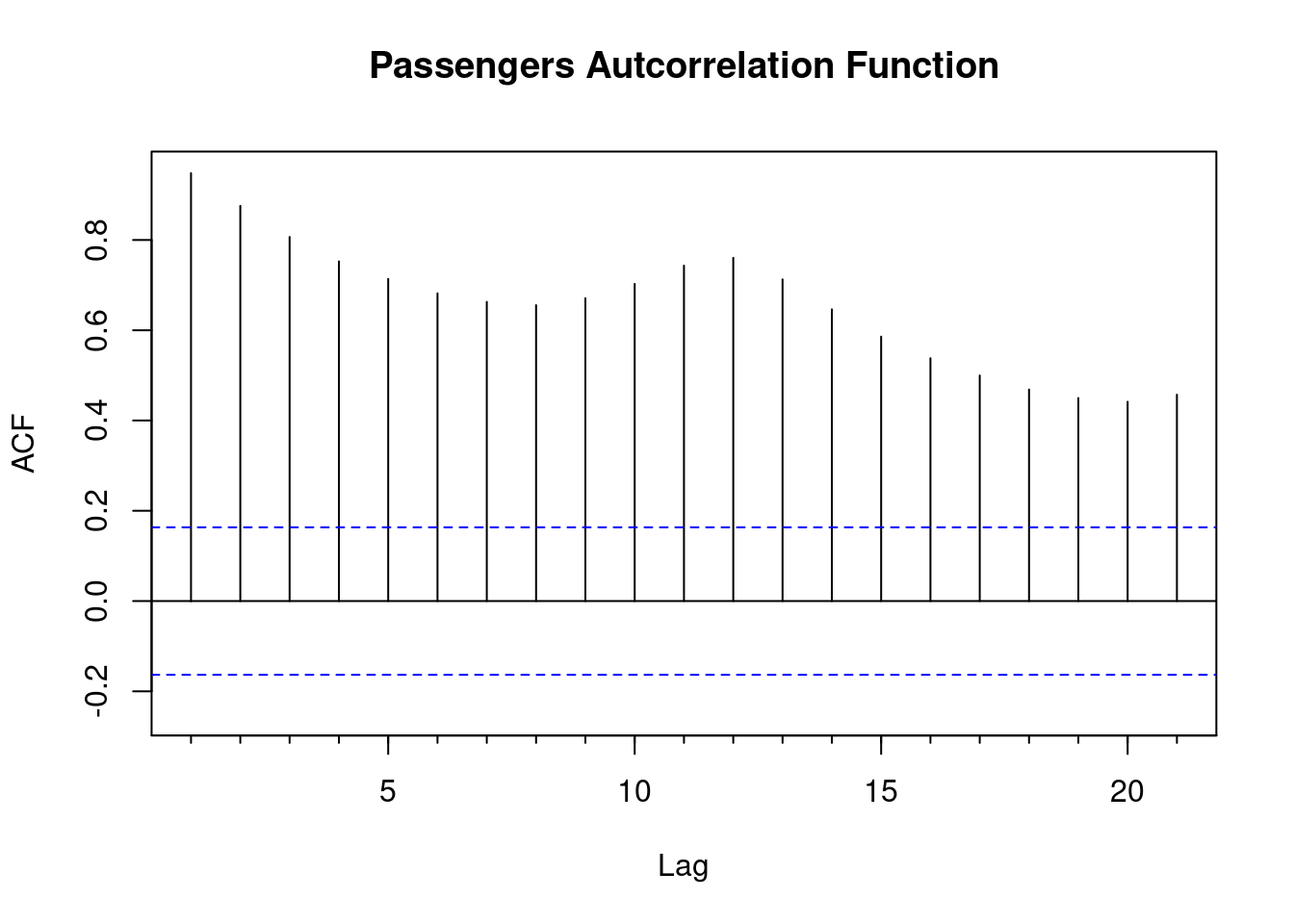

• Partial Autocorrelation Function:
  • The partial correlation of the series at time t with the series at time t-k given all the information between t-k….t
  • Same critical regions as ACF
  • ACF vs PACF:
    • Redundant correlations appear in ACF
    • PACF correlations show exactly how the kth lagged value is related to the current point
    • PACF helps you know how long a time series needs to be to capture dynamics you want to model
  • forecast package Pacf()

Pacf(new$AirPassengers,main='Passengers Partial Autcorrelation Function')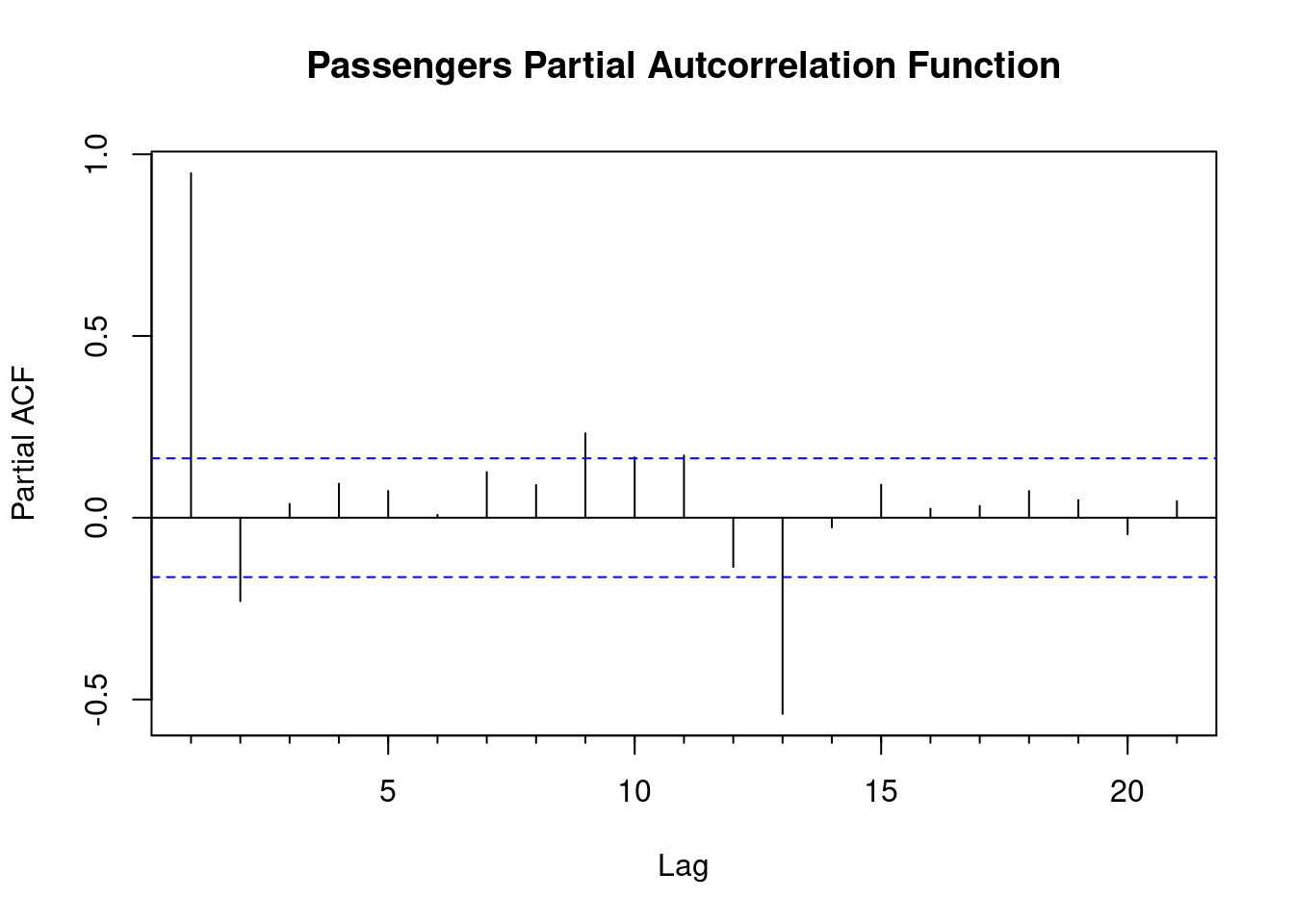

• Observations:
  • The ACF fails to trail off after a certain lag, indicating clear trend
  • PACF shows strong significance at around lag 12, coinciding with Christmas, a seasonal peak that is to be expected.
  • Behavior of the PACF and ACF vital in determining parameters for time series ARIMA models and many others.

Now you are ready to get started with time series data!

References

• https://www.statology.org/exponential-moving-average-in-r/
• https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc442.htm
• https://learning.oreilly.com/library/view/practical-time-series/9781492041641/ch02.html